初中数学七年级知识点总结4.4：立方根的定义表示方法及其性质

初中数学七年级知识点总结4.4：立方根的定义表示方法及其性质

一般地，如果一个数的立方等a，那么这个数叫做a的立方根或三次方根，也就是说，如果x³=a，那么x叫做a的立方根。

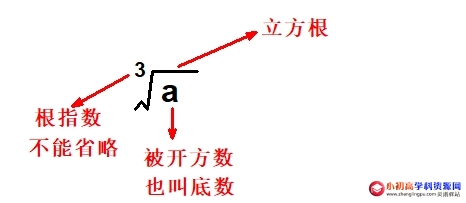
一个数a的立方根，用符号“3√a”表示，读作“三次根号a”，其中a是被开方数，3是根指数（不能省略）。

1、正数的立方根是正数；

2、负数的立方根是负数；

3、0的立方根是0。

也就是说任何一个数有有立方根，而且只有一个立方根，立方根等于本身的数有0，±1。

\[\begin{gathered}
\sqrt[3]{{ - a}} = - \sqrt[3]{a},\sqrt[3]{{{a^3}}} = a,{\left( {\sqrt[3]{{ - a}}} \right)^3} = - a,{\left( {\sqrt[3]{a}} \right)^3} = a \hfill \\若a = b, 则\sqrt[3]{a} = \sqrt[3]{{\text{b}}}, 那么反过来如果\sqrt[3]{a} = \sqrt[3]{{\text{b}}}  则a = b \hfill \\
\end{gathered} \]

求一个数的立方根的运算，叫做开立方，开立方与立方互为逆运算，可以根据这咱关系求一个数的立方根，任何数都有立方根，并且只有一个立方根。