张灵谱
阅读模式
例题1：实数a在数轴上的对应点A的位置如图所示，化简\(\displaystyle \left| {a-1} \right|+\sqrt{{{{{\left( {a-2} \right)}}^{2}}}}\)
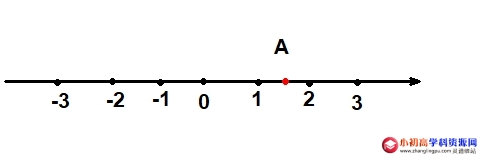
解：据题意得：1<a<2
∴ 原式\(\displaystyle =a-1+\left| {a-2} \right|\)
\(\displaystyle =a-1-a+2\)
\(\displaystyle =1\)
例题2：已知实数a,b在数轴上表示的点如图所示，试化简下列各式
（1）、\(\displaystyle \sqrt{{{{a}^{2}}}}+\left| {ab} \right|\)
（2）、\(\displaystyle \left| {a+b} \right|+\left| {a-b} \right|\)
解析：通过图示可以看出a,b互为相反数
解：
（1）、原式\(\displaystyle =-a-ab\)
\(\displaystyle =-a+{{a}^{2}}\)
（2）、原式\(\displaystyle =0+b-a\)
\(\displaystyle =-2a\)
例题3：已知数a,b,c在数轴上的位置如图所示，化简\(\displaystyle \sqrt{{{{a}^{2}}}}-\left| {a+c} \right|+\sqrt{{{{{\left( {c-b} \right)}}^{2}}}}-\left| {-b} \right|\)
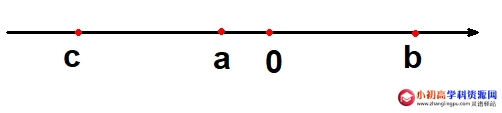
原式\(\displaystyle =\left| a \right|-\left| {a+c} \right|+\left| {c-b} \right|-\left| {-b} \right|\)
\(\displaystyle =-a+a+c-c+b-b\)
\(\displaystyle =-a+a+c-c+b-b\)
我的微信
微信号已复制
⇐ 加微信，获取海量学习资源！
专注小初高数学教学研究20余年，拥有优质的学科资源，如有需要请联系张老师！