初中数学七年级知识点总结5.2:坐标平面内点的坐标的特点

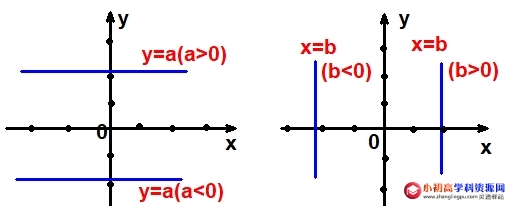
平行于x轴的直线上的所有点的纵坐标相同,平行于y轴的直线上的点的横坐标相同(如下图)
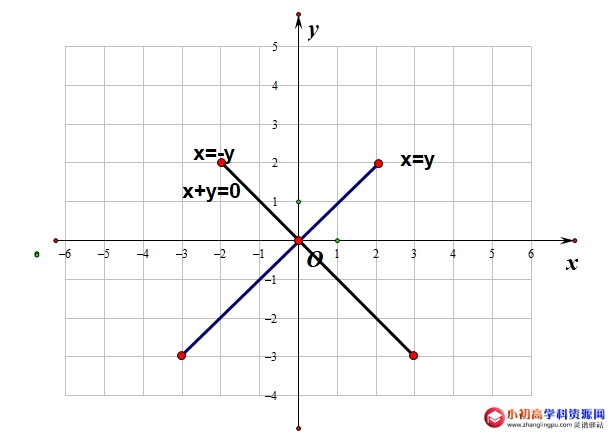
点P(x,y)在第一、三象限两坐标轴夹角的平分线上⇔ x=y(纵横坐标相等)
点P(x,y)在第二、四象限两坐标轴夹角的平分线上⇔ x=-y(纵横坐标互为相反数)
1、点P(x,y)到原点的距离为\(\displaystyle \sqrt{{{{x}^{2}}+{{y}^{2}}}}\)
2、同一坐标轴上的两点之间的距离为\(\displaystyle \left| {{{x}_{1}}-{{x}_{2}}} \right|\)或\(\displaystyle \left| {{{y}_{1}}-{{y}_{2}}} \right|\)
3、平行于坐标轴的直线上的两点之间的距离为\(\displaystyle \left| {{{x}_{1}}-{{x}_{2}}} \right|\)或\(\displaystyle \left| {{{y}_{1}}-{{y}_{2}}} \right|\)
4、不同坐标轴上的两两点A(x,0),B(0,y)之间的距离为\(\displaystyle \sqrt{{{{x}^{2}}+{{y}^{2}}}}\)
拓展:平面直角坐标系中任意两点A(x1,y1),B(x2,y2)之间的距离为\(\displaystyle \sqrt{{{{{\left( {{{x}_{1}}-{{x}_{2}}} \right)}}^{2}}+{{{\left( {{{y}_{1}}-{{y}_{2}}} \right)}}^{2}}}}\)
中点坐标公式,AB的中点坐标为\(\displaystyle \left( {\frac{{{{x}_{1}}+{{x}_{2}}}}{2},\frac{{{{y}_{1}}+{{y}_{2}}}}{2}} \right)\)


